Hado van Hasselt
DataRater: Meta-Learned Dataset Curation
May 23, 2025Abstract:The quality of foundation models depends heavily on their training data. Consequently, great efforts have been put into dataset curation. Yet most approaches rely on manual tuning of coarse-grained mixtures of large buckets of data, or filtering by hand-crafted heuristics. An approach that is ultimately more scalable (let alone more satisfying) is to \emph{learn} which data is actually valuable for training. This type of meta-learning could allow more sophisticated, fine-grained, and effective curation. Our proposed \emph{DataRater} is an instance of this idea. It estimates the value of training on any particular data point. This is done by meta-learning using `meta-gradients', with the objective of improving training efficiency on held out data. In extensive experiments across a range of model scales and datasets, we find that using our DataRater to filter data is highly effective, resulting in significantly improved compute efficiency.
Wasserstein Policy Optimization
May 01, 2025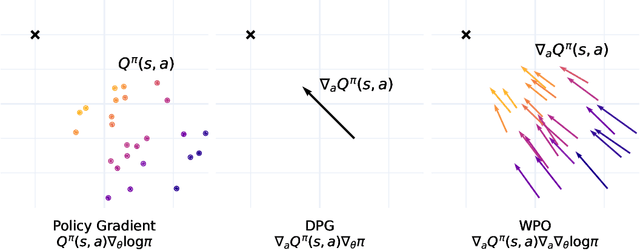
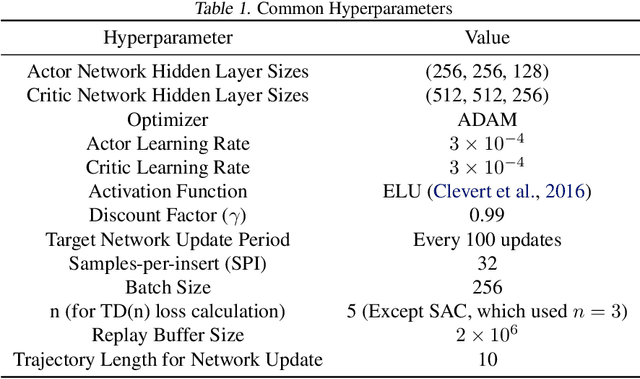
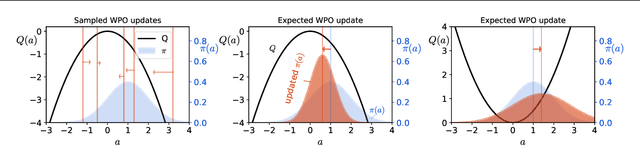
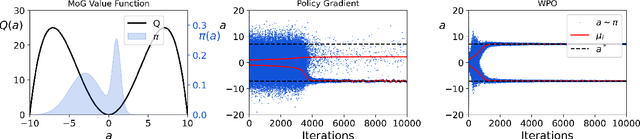
Abstract:We introduce Wasserstein Policy Optimization (WPO), an actor-critic algorithm for reinforcement learning in continuous action spaces. WPO can be derived as an approximation to Wasserstein gradient flow over the space of all policies projected into a finite-dimensional parameter space (e.g., the weights of a neural network), leading to a simple and completely general closed-form update. The resulting algorithm combines many properties of deterministic and classic policy gradient methods. Like deterministic policy gradients, it exploits knowledge of the gradient of the action-value function with respect to the action. Like classic policy gradients, it can be applied to stochastic policies with arbitrary distributions over actions -- without using the reparameterization trick. We show results on the DeepMind Control Suite and a magnetic confinement fusion task which compare favorably with state-of-the-art continuous control methods.
Scalable Meta-Learning via Mixed-Mode Differentiation
May 01, 2025



Abstract:Gradient-based bilevel optimisation is a powerful technique with applications in hyperparameter optimisation, task adaptation, algorithm discovery, meta-learning more broadly, and beyond. It often requires differentiating through the gradient-based optimisation process itself, leading to "gradient-of-a-gradient" calculations with computationally expensive second-order and mixed derivatives. While modern automatic differentiation libraries provide a convenient way to write programs for calculating these derivatives, they oftentimes cannot fully exploit the specific structure of these problems out-of-the-box, leading to suboptimal performance. In this paper, we analyse such cases and propose Mixed-Flow Meta-Gradients, or MixFlow-MG -- a practical algorithm that uses mixed-mode differentiation to construct more efficient and scalable computational graphs yielding over 10x memory and up to 25% wall-clock time improvements over standard implementations in modern meta-learning setups.
General Uncertainty Estimation with Delta Variances
Feb 20, 2025



Abstract:Decision makers may suffer from uncertainty induced by limited data. This may be mitigated by accounting for epistemic uncertainty, which is however challenging to estimate efficiently for large neural networks. To this extent we investigate Delta Variances, a family of algorithms for epistemic uncertainty quantification, that is computationally efficient and convenient to implement. It can be applied to neural networks and more general functions composed of neural networks. As an example we consider a weather simulator with a neural-network-based step function inside -- here Delta Variances empirically obtain competitive results at the cost of a single gradient computation. The approach is convenient as it requires no changes to the neural network architecture or training procedure. We discuss multiple ways to derive Delta Variances theoretically noting that special cases recover popular techniques and present a unified perspective on multiple related methods. Finally we observe that this general perspective gives rise to a natural extension and empirically show its benefit.
Normalization and effective learning rates in reinforcement learning
Jul 01, 2024



Abstract:Normalization layers have recently experienced a renaissance in the deep reinforcement learning and continual learning literature, with several works highlighting diverse benefits such as improving loss landscape conditioning and combatting overestimation bias. However, normalization brings with it a subtle but important side effect: an equivalence between growth in the norm of the network parameters and decay in the effective learning rate. This becomes problematic in continual learning settings, where the resulting effective learning rate schedule may decay to near zero too quickly relative to the timescale of the learning problem. We propose to make the learning rate schedule explicit with a simple re-parameterization which we call Normalize-and-Project (NaP), which couples the insertion of normalization layers with weight projection, ensuring that the effective learning rate remains constant throughout training. This technique reveals itself as a powerful analytical tool to better understand learning rate schedules in deep reinforcement learning, and as a means of improving robustness to nonstationarity in synthetic plasticity loss benchmarks along with both the single-task and sequential variants of the Arcade Learning Environment. We also show that our approach can be easily applied to popular architectures such as ResNets and transformers while recovering and in some cases even slightly improving the performance of the base model in common stationary benchmarks.
Disentangling the Causes of Plasticity Loss in Neural Networks
Feb 29, 2024Abstract:Underpinning the past decades of work on the design, initialization, and optimization of neural networks is a seemingly innocuous assumption: that the network is trained on a \textit{stationary} data distribution. In settings where this assumption is violated, e.g.\ deep reinforcement learning, learning algorithms become unstable and brittle with respect to hyperparameters and even random seeds. One factor driving this instability is the loss of plasticity, meaning that updating the network's predictions in response to new information becomes more difficult as training progresses. While many recent works provide analyses and partial solutions to this phenomenon, a fundamental question remains unanswered: to what extent do known mechanisms of plasticity loss overlap, and how can mitigation strategies be combined to best maintain the trainability of a network? This paper addresses these questions, showing that loss of plasticity can be decomposed into multiple independent mechanisms and that, while intervening on any single mechanism is insufficient to avoid the loss of plasticity in all cases, intervening on multiple mechanisms in conjunction results in highly robust learning algorithms. We show that a combination of layer normalization and weight decay is highly effective at maintaining plasticity in a variety of synthetic nonstationary learning tasks, and further demonstrate its effectiveness on naturally arising nonstationarities, including reinforcement learning in the Arcade Learning Environment.
A Survey of Temporal Credit Assignment in Deep Reinforcement Learning
Dec 02, 2023



Abstract:The Credit Assignment Problem (CAP) refers to the longstanding challenge of Reinforcement Learning (RL) agents to associate actions with their long-term consequences. Solving the CAP is a crucial step towards the successful deployment of RL in the real world since most decision problems provide feedback that is noisy, delayed, and with little or no information about the causes. These conditions make it hard to distinguish serendipitous outcomes from those caused by informed decision-making. However, the mathematical nature of credit and the CAP remains poorly understood and defined. In this survey, we review the state of the art of Temporal Credit Assignment (CA) in deep RL. We propose a unifying formalism for credit that enables equitable comparisons of state of the art algorithms and improves our understanding of the trade-offs between the various methods. We cast the CAP as the problem of learning the influence of an action over an outcome from a finite amount of experience. We discuss the challenges posed by delayed effects, transpositions, and a lack of action influence, and analyse how existing methods aim to address them. Finally, we survey the protocols to evaluate a credit assignment method, and suggest ways to diagnoses the sources of struggle for different credit assignment methods. Overall, this survey provides an overview of the field for new-entry practitioners and researchers, it offers a coherent perspective for scholars looking to expedite the starting stages of a new study on the CAP, and it suggests potential directions for future research
On the Convergence of Bounded Agents
Jul 20, 2023Abstract:When has an agent converged? Standard models of the reinforcement learning problem give rise to a straightforward definition of convergence: An agent converges when its behavior or performance in each environment state stops changing. However, as we shift the focus of our learning problem from the environment's state to the agent's state, the concept of an agent's convergence becomes significantly less clear. In this paper, we propose two complementary accounts of agent convergence in a framing of the reinforcement learning problem that centers around bounded agents. The first view says that a bounded agent has converged when the minimal number of states needed to describe the agent's future behavior cannot decrease. The second view says that a bounded agent has converged just when the agent's performance only changes if the agent's internal state changes. We establish basic properties of these two definitions, show that they accommodate typical views of convergence in standard settings, and prove several facts about their nature and relationship. We take these perspectives, definitions, and analysis to bring clarity to a central idea of the field.
A Definition of Continual Reinforcement Learning
Jul 20, 2023Abstract:In this paper we develop a foundation for continual reinforcement learning.
Exploration via Epistemic Value Estimation
Mar 07, 2023



Abstract:How to efficiently explore in reinforcement learning is an open problem. Many exploration algorithms employ the epistemic uncertainty of their own value predictions -- for instance to compute an exploration bonus or upper confidence bound. Unfortunately the required uncertainty is difficult to estimate in general with function approximation. We propose epistemic value estimation (EVE): a recipe that is compatible with sequential decision making and with neural network function approximators. It equips agents with a tractable posterior over all their parameters from which epistemic value uncertainty can be computed efficiently. We use the recipe to derive an epistemic Q-Learning agent and observe competitive performance on a series of benchmarks. Experiments confirm that the EVE recipe facilitates efficient exploration in hard exploration tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge